|
Как уже говорилось, наиболее популярной формой социокультурных процессов являемся прямая линия, отражающая линейные представления о ходе социального времени. Однако мыслителей всех времен привлекали также циклическая модель социального времени, предполагающая периодическое повторение определенных фаз развития, рекуррентное возвращение к исходному возвращению к исходному состоянию. Простейшая траектория циклического типа в виде синусоидальной кривой с горизонтальным трендом приведена на рис. 5.9, а с линейно возрастающим трендом – на рис. 5.10. Циклическая траектория количественной переменной не обязательно точно соответствует графику математической синусоиды – период и амплитуда колебаний могут со временем меняться[7].
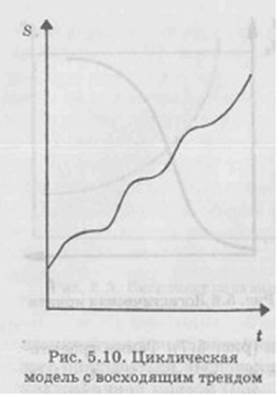
Естественно, говорить о точном следовании синусоиде в случае качественной переменной просто неуместно. Именно качественные переменные, как правило, имеют в виду, рассматривая развитие процесса по спирали. Известно, что образ спирали обладает большой генеративной силой, весьма способствует инсайту, благодаря чему довольно часто фигурирует в трудах обществоведов в качестве одной из базовых метафор социальных изменений. Как геометрический объект спираль изображается в трехмерном пространстве, одной координатой которого является время t, а две другие координаты соответствуют двум показателям S1 и S2, характеризующим эволюцию наблюдаемой системы V. Причем следует обязательно учитывать то, что спираль отражает динамику взаимодействия именно двух взаимосвязанных факторов[8].
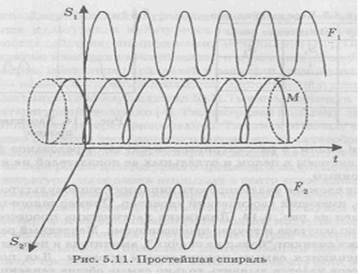
Пример спирали M, приведенной на рис. 5. 11, показывает, что в простейшем случае спираль можно представить в виде линии, наматываемой на цилиндр (изображен штриховой линией). Ясно, что цилиндр не обязательно расположен горизонтально, он может быть и наклонен.
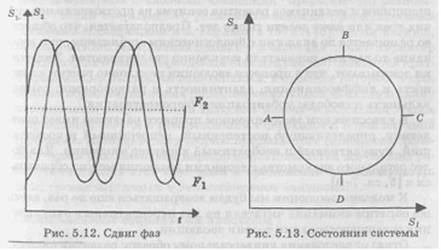
Чтобы более наглядно представить ход изменения значений факторов S1 и S2, спроектируем спираль сначала на плоскость (S1; t), a затем на плоскость (S2; t). Получим две траектории синусоидального типа F1 и F2. Если мы попробуем изобразить их на одном графике с общей осью времени, то сразу заметим, что фазы колебаний факторов S1 и S2 не совпадают (рис. 5.12). Чтобы наглядно представить себе взаимосвязь факторов S1 и S2, спроектируем спираль на плоскость (S1; S2). Очевидно, что в этом случае получим круг, изображенный на рис. 5.13.
На рисунке движение по спирали становится движением по кругу по часовой стрелке (в данном случае время t можно рассматривать как параметр*). Чередование фаз изменения факторов S1 и S2 при движении по секторам AB; ВС; CD; DA круга представлено в табл. 5.2.
* Простейшая винтовая линия в пространстве может быть представлена в параметрическом виде: х = acost; у = asint; г = ct.
Таблица 5.2. Чередование фаз |
Сектор |
Изменение фазы | |
|
S1 |
S2 | |
AB |
+ |
+ | |
ВС |
+ |
- | |
CD |
- |
- | |
DA |
- |
+ |
Подобные статьи:
Гарвардский исследовательский центр по креативному альтруизму.
Гарвардский исследовательский центр по креативному альтруизму был официально открыт в феврале 1949г. В основу создания Центра были положены два основных предположения:
1. Ни один из существующих рецептов, как избежать международных военн ...
Сущность урбанизации и показатели урбанизированности населения Земли
Возникновение и постоянное увеличение площади и численности населения городов, приобретение сельскими поселениями городских признаков, повышение роли городов в социально- экономическом развитии общества, формирование городского населения, ...
Роль СМИ в политической жизни общества
Для выяснения сущности средств массовой информации необходимо уточнить, что понимают под средствами массовой информации.
Под средствами массовой информации понимаются газеты, журналы, теле- и радиопрограммы, кинодокументалистика, иные пе ...
|